Basiswissen Bruchrechnen
Wer braucht heute Bruchrechnen? Mal abgesehen von der Schulzeit braucht man Bruchrechnung im späteren Leben kaum noch. Doch manchmal kommt der Tag, wo zumindest das Basiswissen von Mathematik abgefragt wird. Ein Eignungstest versperrt Ihnen den Zugang zum neuen Job?
Ein Eignungstest versperrt Ihnen den Zugang zum neuen Job?
Keine Panik! Hier wird Ihnen geholfen! Meistens werden in Eignungstests einfach ein paar Grundrechenarten sowie deutsch und Allgemeinbildung abgefragt. Kann jeder schaffen! Jedoch sollte man einen Test nicht auf die leichte Schulter nehmen. Denn immerhin kann so ein Test entscheidend über Ihre berufliche Zukunft sein.
Direkt zur Rechenaufgabe mit Brüchen:
Bruch mit Multiplikation
Bruch mit Division
Bruch mit Addition
Bruch mit Subtraktion
Bruch kürzen
Bruch in Dezimal
Meine Empfehlung:
Der Testtrainer, geeignet für alle Arten von Tests
Für jemanden der eine Umschulung beabsichtigt, wird mit ziemlicher Sicherheit von der Arbeitsagentur für Arbeit oder von der deutschen Rentenversicherung zu einen Eignungstest eingeladen. Es warten auf den Umschüler neben anderen Testaufgaben auch ein paar hübsche Rechenaufgaben. Alles nur um festzustellen, ob dieser jemand für Berufe der unteren, mittleren oder höheren Stufe geeignet ist.
Wer sich von der Schule aus direkt auf eine Ausbildungsstelle bewirbt, wird in der Regel mit anderen Bewerbern auch zu einen Eignungstest eingeladen. Hier empfiehlt es sich nicht nur in den Grundrechenarten, deutsch und der Allgemeinbildung fit zu sein. Am besten auch vorab wissenswertes zum Job in Erfahrung bringen.
Das können ganz banale Dinge sein. Für eine Ausbildung im Computerbereich, IT-Systeme u.s.w. ist es zum Vorteil gewisse Grundkenntnisse über die Bauteile und deren Zusammenhänge zu haben. Oder beim Job in der Mediengestaltung sollte man bei deutschen Wortgruppen, Wortbeziehungen fit sein. Auch räumliches Denken und natürlich einen englischen Text sinngemäß zu übersetzen, kann ein Bestandteil eines Einstellungstests sein. Jetzt genug über Einstellungstest bei Jobs geredet.
Dann fangen wir doch gleich mal mit einer Bruchrechnung an. Es ist einfacher als man denkt. Bereits einmal in der Schule erlerntes später wieder aufzufrischen ist natürlich einfacher als wenn man das erste Mal vor einer Bruchrechnung sitzt. Es geht hier in erster Linie um den Wiedereinstieg ins Bruchrechnen. Praktisch die Grundkenntnisse in Mathe auffrischen.
Zwei Brüche multiplizieren
Mir erscheint der Wiedereinstieg mit dem Multiplizieren von zwei Brüchen am einfachsten. Darum beginnen wir hiermit. Brüche multiplizieren rechnen…
Eine Beispielaufgabe wie sie im Eignungstest vorkommen kann:
 Bei einer Rechenaufgabe, wo zwei Brüche multipliziert werden sollen, können Sie nicht viel verkehrt machen.
Bei einer Rechenaufgabe, wo zwei Brüche multipliziert werden sollen, können Sie nicht viel verkehrt machen.
Sie müssen nur den ersten Zähler mal den zweiten Zähler multiplizieren und das Ergebnis über den Bruchstrich schreiben. In dem Fall ist das die Zahl 20.
Das selbe machen Sie mit den Nenner vom ersten Bruch mal den zweiten Nenner multiplizieren und das Ergebnis unter dem Bruchstrich schreiben. Das wäre dann die Zahl 28. Fertig!
In der Regel wird der Operator für Multiplikation zwischen die Brüche geschrieben. In meinen Beispielen steht die zu berechnende Aufgabe immer oben und darunter wird der Rechenweg ausgeführt. Aus einem roten Mal-Zeichen wurden in dem darunter stehenden Rechenweg zwei rote Mal-Zeichen. Das soll nur zur besseren Orientierung dienen.
Bevor es jetzt mit Bruchrechnen richtig weiter geht, möchte ich nur mal kurz ein paar Basics auffrischen.
Woraus besteht eine Bruchrechnung?
Der Bruch selbst besteht aus einer Zahl über dem Bruchstrich. Diese Zahl bezeichnet man als Zähler. Dann wäre da die Zahl unterm Bruchstrich. Diese Zahl bezeichnet man als Nenner. Zwischen den Brüchen steht ein Operator-Zeichen. Das ist in der Regel eines der 4 Grundrechenarten. Also Operator-Zeichen wie Plus +, Minus -, Mal * und Geteilt ÷
So, jetzt kommen wir beim Bruchrechnen zur nächsten Rechenaufgabe.
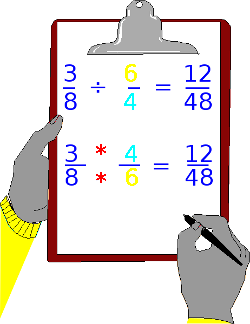
Zwei Brüche geteilt rechnen
Zwei Brüche teilen ist im Schwierigkeitsgrad eine Stufe höher.
Es wird zwar im Prinzip auch nichts anderes gemacht als Multipliziert. Jedoch mit einen Unterschied und den sollten Sie sich gut merken. Siehe Bild 2:
Haben Sie als Operator einen Teiler in Ihrer Bruch-Rechenaufgabe, dann drehen Sie den nachfolgenden Bruch einfach um. Hier im Bild farblich markiert.
Aus dem gelben Zähler wird ein Nenner und aus dem türkis farbigen Nenner wird ein Zähler. Aus dem Geteilt-Zeichen wird im zweiten Rechenschritt das Zeichen für die Multiplikation. Hier rot dargestellt.
Schauen Sie sich diese Aufgabe in aller Ruhe an. Oben die Rechenaufgabe mit den bereits eingefärbten Zahlen und darunter der fertige Rechenweg mit den umgestellten Bruch. Denken Sie immer daran, ist der Operator ein Teiler, dann wird der nachfolgende Bruch einmal umgedreht. Zähler nach unten und Nenner nach oben.
Um an das Ergebnis zu gelangen, müssen Sie im Anschluss nur noch die beiden Zahlen über den Bruchstrich miteinander multiplizieren und das selbe auch mit den unteren beiden Zahlen tun. Fertig!
Brüche addieren
Wenn Sie sich das Multiplizieren und Dividieren von Brüchen verinnerlicht haben, dann können Sie rund die Hälfte der Aufgaben lösen und holen so schon mal beim Eignungstest wichtige Punkte.
Denn der nächste Schritt ist Brüche addieren. Da kann man schon mal unter Zeitdruck den einen oder anderen Fehler machen. Also, wenn Bruchrechnen nicht so zu Ihren Stärken zählt, dann sollten Sie erst mit anderen Matheaufgaben weiter machen und wenn am Schluss der Prüfungszeit noch Zeit übrig sein sollte, dann können Sie die restliche Zeit damit verbringen, diese Bruchrechnungen zu lösen.
Hier kommt die Addition von Brüchen

Bei der Addition von Brüchen ist es ganz wichtig, zuerst alle Brüche auf den gleichen Nenner zu bringen.
In diesem Beispiel links – Bild 3 – sind zwei Brüche mit ungleichen Nennern. Der erste Schritt ist es den Nenner vom ersten Bruch in einer separaten Rechnung mit dem zweiten Bruch zu multiplizieren.
Das heißt:
Der Zähler vom ersten Bruch wird erst einmal nicht weiter beachtet. Siehe Bild 3 farblich dargestellt.
Der Nenner vom ersten Bruch wird in der Rechenaufgabe als eigener Bruch dargestellt. Der Nenner wird sowohl unter als auch über die Bruchstrich-Linie geschrieben. Dann wird der zweite Bruch im Original eins zu eins übernommen. Jetzt werden diese zwei Brüche wie eine ganz normale Aufgabe mit Multiplikation behandelt. Wie das geht, steht in der allerersten Aufgabe. Das war der erste Schritt in Richtung Brüche addieren.
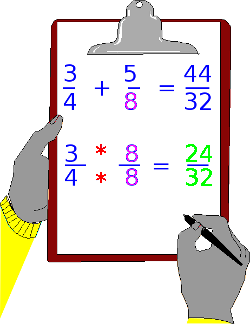
Jetzt kommen wir zum zweiten Schritt. Denn das was jetzt mit dem ersten Bruch passiert ist, muss auch mit dem zweiten Bruch gemacht werden.
Hierzu lassen wir den ersten Bruch original so wie er in der Aufgabe steht. Der zweite Bruch wird geändert. Der Nenner vom zweiten Bruch wird jetzt auch die Stelle des Zählers einnehmen. Siehe farbig markierte Zahl im vierten Bild.
Der erste Bruch wird jetzt mit den Nenner vom zweiten Bruch multipliziert und siehe da, wir haben beide Brüche auf einen Nenner gebracht.
Als Merksatz kann man sagen: „Bei Addition von Brüchen müssen erst einmal alle Brüche auf einen Nenner gebracht werden in dem man jeden Bruch mit dem Nenner des anderen Bruchs multipliziert. Erst dann kann man die Brüche addieren.“
Kleiner Hinweis: Wenn in der Rechenaufgabe die Nenner bereits gleich sind, dann können die Zähler direkt addiert werden. Aber das wird bei den Testaufgaben in Einstellungstests bzw. Eignungstests wohl kaum vorkommen. Darauf sollten Sie besser nicht hoffen.
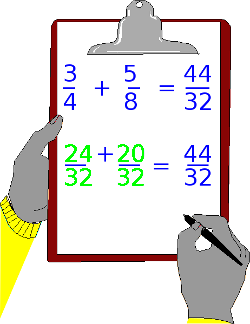
Der Vollständigkeit hier der letzte Schritt in der Addition von Brüchen.
Nachdem beide Brüche auf den gleichen Nenner gebracht wurden, kann nun die eigentliche Rechenoperation durchgeführt werden.
Hierbei gibt es noch eine Kleinigkeit zu beachten. Die Addition der beiden Brüche geschieht nur im Bereich Zähler.
Die Nenner werden nicht addiert!
Zum besseren Verständnis:
Der Nenner gibt bei einer Bruchaufgabe nur den Hinweis auf die Anzahl der Teile, aus der ein ganzer Bruch besteht.
Da wir die Brüche auf den gleichen Nenner gebracht haben, geben beide Brüche die gleiche Anzahl von Teilen vor, die es braucht um ein Ganzes zu werden.
Ein Beispiel:
Ein 3/4 Bruch bedeutet, dass nur ein (1) Teil zum ganzen fehlt. Also 4/4 wären ein Ganzes. Nehme ich zwei (2) Teile vom 4/4 weg, so hätte ich 2/4 und noch einmal 2/4 und man könnte auch sagen, 1/2 und 1/2 Bruch.
Anteile die ich von einem Bruch wegnehme, stehen nicht im Luftleeren Raum. Ich muss die Teile, die ich von einen Bruch wegnehme, auch immer eine Bezugsgröße hinzufügen. Die Bezugsgröße sagt aus, wie groß die Teile sind. In dem Beispiel mit den 4/4 Bruch muss ich die 2 Teile in der Größe definieren. Die Größe finde ich im Nenner, von dem die Teile sind. Also ein Teil (1) ist ein viertel (1/4) groß.
Deshalb interessiert uns bei der Addition von Brüchen nur die Anzahl der Zähler (Teile) aus der ein Bruch besteht. In unserer Beispielrechnung haben wir als Ergebnis mehr Teile als für einen ganzen Bruch nötig sind. Das erkennt man daran, dass der Zähler größer als der Nenner ist. Man kann Brüche auch kürzen. Aber dazu später mehr.
Können Sie noch?
Geht noch eine Bruchrechnung?
Eine hätte ich noch für Sie.
Eine Bruchrechnung mit drei Brüchen 🙂
Addieren und Subtrahieren von Brüchen
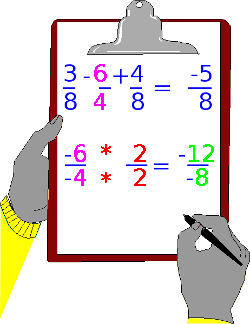
Eine sehr beliebte Konstellation von Rechen-Aufgaben ist bei Eignungstests das Rechnen von drei Brüchen. Sozusagen das Highlight!
Was gibt es dabei zu beachten?
Nun, wie immer der Nenner.
Meistens besteht so eine Bruchaufgabe aus Brüchen mit dem Operator Plus (+) und einen Bruch mit dem Operator Minus (-).
In unserem Beispiel im Bild 6 sehen Sie 2 Brüche mit gleichen Nenner – das ist gut und spart Rechenarbeit – und nur ein Bruch mit einen anderen Nenner. Auf diesen Bruch müssen wir uns konzentrieren.
Achten Sie genau was in der Rechnung passiert. Den lilafarbigen Bruch habe ich darunter zu einer neuen Aufgabe gemacht. Der Bruch wird multipliziert mit der Zahl Zwei (2) und raus kommt ein 12/8 Bruch.
Was ist geschehen?
Es geht darum, beim Addieren bzw. Subtrahieren von Brüchen zuvor alle Brüche einer Aufgabe auf den gleichen Nenner zu bringen. In der Aufgabe haben wir zwei Brüche mit den Nenner 8 und nur einen Bruch mit den Nenner 4. Also müssen wir den kleineren Nenner an die großen Nenner anpassen.
Dazu schauen wir, wie oft der kleine Nenner in die großen Nenner hineinpasst. In unserem Fall ist die 4 genau zweimal in der 8 enthalten. Also wählen wir den Multiplikator 2 und rechnen den Bruch ganz normal durch. Als Ergebnis erhalten wir einen Bruch von 12/8. Das wäre geschafft!
Etwas ganz wichtiges zum negativen Operator! Schreiben Sie den Operator mit in die Zwischenrechnung. Schnell hat man ein Minuszeichen übersehen und plötzlich wird aus Minus ein positiver Bruch und die Aufgabe würde am Ende falsch berechnet werden. Ganz Wichtig! Achten Sie auf die Vorzeichen eines Bruches.
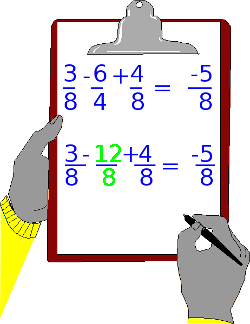
In unserem siebten Bild sehen Sie die Fortsetzung. Der Bruch wurde vom Nenner her an die beiden anderen Brüche angepasst. Siehe grüner Bruch.
Jetzt folgt eine ganz normale Addition und Subtraktion der Brüche.
Bei der Berechnung ist eine kleine Schwierigkeitsstufe eingebaut. Die besonders auf die Konzentration abzielt.
Gerade wenn man im Prüfungsstress ist, können derart kleine Fehler passieren. Aber Sie haben ja aufgepasst und das Minuszeichen immer schön mit geschrieben. Auf den ersten Blick kann man schön sehen, dass in den Zählern 7 positive Brüche 12 negativen gegenüber stehen.
Das ist jetzt wie im richtigen Leben. Hat man Schulden, in dem Fall -12 und rechnet zum Tilgen der Schulden +7 kommt als Ergebnis immer noch eine Restschuld von -5 im Zähler heraus. Alles klar?
Im Prinzip haben Sie jetzt das nötige Wissen über Bruchrechnen und sind für Prüfungsaufgaben dieser Art gut gerüstet. Vielleicht interessiert Sie noch wie man einen Bruch kürzt?
Brüche kürzen
Einen großen Bruch zu kürzen ist relativ einfach!
Unser Beispiel-Bruch lautet: 14/63
Alles was Sie jetzt nur machen müssen, ist zu schauen, durch welche Zahl sich der Zähler und Nenner teilen lässt. In unserem Beispiel ist der Zähler die Zahl 14 und diese lässt sich gut durch die Zahl 7 teilen. Als Ergebnis erhalten wir die Zahl 2. Mit der 7 rechnen wir jetzt die Aufgabe weiter.
Als nächstes teilen wir den Nenner – die Zahl 63 – durch die Zahl 7 und erhalten eine neue Zahl. Die lautet 9 und steht für den neuen Nenner.
Der gekürzte Bruch lautet 2/9 und wir sind mit der Rechenaufgabe fertig!
Manchmal möchte man auch von seinen Testkandidaten einen Bruch als Dezimalzahl dargestellt bekommen. Wie das geht, sehen Sie im folgenden Beispiel:
Bruch in Dezimalzahl
Einen Bruch in Dezimalzahl umwandeln ist auch relativ einfach. Als ersten Schritt schreibt man den Bruch in eine Zeile. Dann teilt man den Zähler durch den Nenner und fertig ist die Dezimalzahl.
Ein Beispiel:
Der Bruch lautet: 1/2
Den Bruchstrich ersetzen Sie durch ein Geteilt-Zeichen (÷)
Der Bruch steht so auf der Zeile: 1 ÷ 2 =
Als Ergebnis bekommen Sie die Dezimalzahl 0,5 heraus und Sie sind fertig!
Ihre Kenntnisse im Bruchrechnen sind wieder aktuell! 🙂
Ich wünsche Ihnen viel Erfolg beim Eignungstest!
Meine Empfehlung:
Der Testtrainer für jede Art Berufeignungstests
Testtrainer für alle Arten von Einstellungstests, Eignungstests und Berufeignungstests
Von Mery, Marcus
Testerfolg ist keine Glückssache!
…sondern eine Frage der Übung – mit dem Testtrainer. Das unverzichtbare Handbuch für Ausbildung, Studium und Beruf zeigt, wie Sie Ihre Prüfung souverän meistern. Geeignet für alle Arten von Fähigkeits- und Intelligenztests, Eignungs- und Einstellungstests.
Optimal vorbereitet…
– für alle Themenbereiche: Rechtschreibung und Grammatik, Textanalyse, Erörterung, Mathematik, logisches Denken, Konzentration, Intelligenz, Allgemeinwissen und viele mehr
– durch Original-Testfragen: aus den aktuellen Einstellungstests namhafter Unternehmen und des öffentlichen Dienstes
– mit mehr als 2.000 Aufgaben: inklusive ausführlich kommentierter Lösungen und umfassender Bearbeitungshinweise.
Lesen, verstehen und lösen. Bekämpfen Sie Prüfungsstress und Unsicherheit durch gezieltes Training – für eine Prüfung ohne böse Überraschungen!
Weitere Eignungstest-Aufgaben
Hier geht es zu:
Prozentrechnung lernen
Werbung!
Sie lesen gerne handfeste Texte in Form von Büchern?
Dann schauen Sie mal hier:



